LeetCode Used Data Structure
Table of Contents
1 Heap
A heap is a structure that the value in the parent node is always greater or equal to its children.
Well, it can also be defined as the parent is less or equal to its children.
In C++ standard library, the priority_queue is organized as the top is the greatest, so lets just use this definition.
The heap must be of the shape of a complete binary tree. Meaning only the last layer can miss some leafs at the end.
1.1 priority queue
We can use a heap data structure to implement a priority queue. Instead of FIFO, the order that come out of priority queue is by its priority, a.k.a. value.
1.1.1 Usage
1.1.1.1 295. Find Median from Data Stream
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.
Design a data structure that supports the following two operations:
- void addNum(int num) - Add a integer number from the data stream to the data structure.
- double findMedian() - Return the median of all elements so far.
Here's a solution that use linked list. So slow.
class MedianFinder { public: // Adds a number into the data structure. void addNum(int num) { if (m_data.empty()) { m_data.push_back(num); m_it = m_data.begin(); } else { std::list<int>::iterator it = m_it; if (*it < num) { while (it != m_data.end() && *it < num) { it++; } m_data.insert(it, num); if (m_data.size() % 2 == 1) { m_it++; } } else if (*it == num) { m_data.insert(it, num); if (m_data.size() % 2 == 0) { m_it--; } } else { while (it != m_data.begin() && *it > num) { it--; } if (it == m_data.begin() && *it > num) { m_data.insert(it, num); } else { it++; m_data.insert(it, num); } if (m_data.size() % 2 == 0) { m_it--; } } } } // Returns the median of current data stream double findMedian() { double ret = 0; std::list<int>::iterator it = m_it; if (m_data.size() % 2 == 0) { ret = *it; ret += *(++it); ret /= 2; return ret; } else { return *it; } } private: std::list<int> m_data; std::list<int>::iterator m_it; };
Instead, using priority queue, we can use two heap for the smaller half and larger half. Some points needs to be careful:
- Since C++ priorityqueue is greatest top, so the larger half can simply use the negative
- But whenever use negative, you need to consider the range of int, so use a long
- when calculate a int divided by a int, cast to double!
- cannot get the top of an empty container!
class MedianFinder { public: void addNum(int num) { if (smaller.empty()) { smaller.push(num); return; } long n = num; if (smaller.size() == larger.size()) { if (larger.top() > -n) { larger.push(-n); smaller.push(-larger.top()); larger.pop(); } else { smaller.push(n); } } else { // smaller have one more if (smaller.top() > n) { smaller.push(n); larger.push(-smaller.top()); smaller.pop(); } else { larger.push(-n); } } } double findMedian() { assert(!smaller.empty()); if (smaller.size() == larger.size()) { return (double)(smaller.top() - larger.top()) / 2; } else { return smaller.top(); } } private: std::priority_queue<long> smaller; std::priority_queue<long> larger; };
This is not very clean code, a more elegant one (Note this will have more push and pop to the heap, so more time overhead):
class MedianFinder3 { public: void addNum(int num) { smaller.push((long)num); larger.push(-smaller.top()); smaller.pop(); if (larger.size() > smaller.size()) { smaller.push(-larger.top()); larger.pop(); } } double findMedian() { assert(!smaller.empty()); return smaller.size() == larger.size() ? (double)(smaller.top() - larger.top()) / 2 : smaller.top(); } private: std::priority_queue<long> smaller; std::priority_queue<long> larger; };
1.2 Implement
Insert:
- First, insert the value at the end of the array, so that we maintain the shape.
- Then, pop the value up by comparing with parent, swap if possible and continue.
Remove:
- first, remove the root, and move the end of the array to the root.
- sink the root down, by comparing with its two children. Swap with the larger child if there is one.
2 TODO Binary Search Tree
3 Other
3.1 Trie
3.1.1 79. Word Search I
Given a 2D board and a word, find if the word exists in the grid. The word can be constructed from letters of sequentially adjacent cell, where "adjacent" cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.
No magic here, try to start from each cell. Recur the four directions, so that the back-tracing is automatic by recurrence.
class Solution { public: bool exist(vector<vector<char>>& board, string word) { if (board.empty() || board[0].empty()) return false; for (size_t i=0;i<board.size();i++) { for (size_t j=0;j<board[0].size();j++) { if (recur(board, word, i, j, 0)) return true; } } return false; } bool recur(vector<vector<char>> &board, string word, int x, int y, int idx) { // std::cout << "recur: " << x << "," << y << "\n"; if (idx >= (int)word.size()) { return true; } if (x < 0 || y < 0 || x >= (int)board.size() || y >= (int)board[0].size()) { // std::cout << " <--" << "\n"; return false; } if (board[x][y] != word[idx]) { // std::cout << " <--" << "\n"; return false; } if (board[x][y] == word[idx]) { char c = board[x][y]; board[x][y] = '\0'; if ( recur(board, word, x+1, y, idx+1) || recur(board, word, x, y+1, idx+1) || recur(board, word, x-1, y, idx+1) || recur(board, word, x, y-1, idx+1) ) return true; board[x][y] = c; return false; } return false; } };
3.1.2 Trie
The implementation is easy, but know when to use it is hard!
class TrieNode { public: TrieNode() { } TrieNode *child(char c) { if (m_map.count(c) == 1) return m_map[c]; return NULL; } TrieNode *addChild(char c) { TrieNode *node = new TrieNode(); m_map[c] = node; return node; } bool isLeaf() { return m_isleaf; } void setLeaf() { m_isleaf = true; } bool hasChild() { return !m_map.empty(); } private: std::map<char, TrieNode*> m_map; bool m_isleaf = false; }; class Trie { public: Trie() { root = new TrieNode(); } // Inserts a word into the trie. void insert(string word) { TrieNode *node = root; for (char c : word) { if (node->child(c)) { node = node->child(c); } else { node = node->addChild(c); } } node->setLeaf(); } // Returns if the word is in the trie. bool search(string word) { TrieNode *node = root; for (char c : word) { if ((node = node->child(c))) { } else { return false; } } if (node->isLeaf()) { return true; } return false; } // Returns if there is any word in the trie // that starts with the given prefix. bool startsWith(string prefix) { TrieNode *node = root; for (char c : prefix) { if ((node = node->child(c))) { } else { return false; } } return true; } private: TrieNode* root; };
3.1.3 212. Word Search II
We only carry the TrieNode, and it should store the word, aka the value.
class Solution { public: vector<string> findWords(vector<vector<char>>& board, vector<string>& words) { // construct a trie for all the words to search // continue to do the recursive method // keep the track of current value // if cannot search it on trie, stop the recursion along this line Trie trie; for (string s : words) { trie.insert(s); } for (int i=0;i<(int)board.size();i++) { for (int j=0;j<(int)board[0].size();j++) { recur(board, i, j, trie.getRoot()); } } vector<string> retv (ret.begin(), ret.end()); return retv; } void recur(vector<vector<char> > &board, int i, int j, TrieNode *node) { if (!node) {return;} if (node->isLeaf()) ret.insert(node->Value()); if (!node->hasChild()) {return;} if (i < 0 || j < 0 || i >= (int)board.size() || j >= (int)board[0].size()) {return;} if (node->child(board[i][j])) { char c = board[i][j]; board[i][j] = '\0'; node = node->child(c); recur(board, i, j-1, node); recur(board, i, j+1, node); recur(board, i-1, j, node); recur(board, i+1, j, node); board[i][j] = c; } else { return; } } private: set<string> ret; };
3.2 prefix tree
Alias: Trie, Prefix Tree, Radix Tree
It is an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings
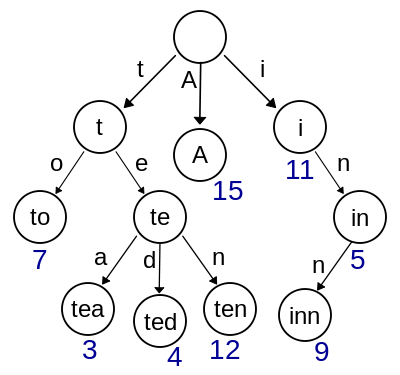
3.2.1 Radix Tree
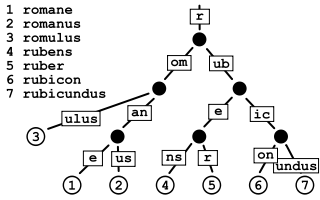
A radix tree (also patricia trie or radix trie or compact prefix tree) is a space-optimized trie data structure where each node with only one child is merged with its parent.
Unlike in regular tries, edges can be labeled with sequences of elements as well as single elements.
3.3 Aho Corasick
It is a multiple string match algorithm. fgrep is based on this.
3.3.1 Construct Trie
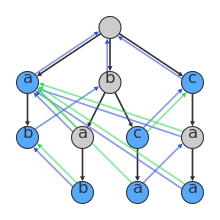
dictionary: {a,ab,bab,bc,bca,c,caa}
3.3.2 Node
The data structure has one node for every prefix of every string in the dictionary. So if (bca) is in the dictionary, then there will be nodes for (bca), (bc), (b), and ().
3.3.3 Color
If a node is in the dictionary then it is blue node. Otherwise it is a grey node.
3.3.4 blue arc
a blue directed "suffix" arc from each node to the node that is the longest possible strict suffix of it in the graph. For example, for node (caa), its strict suffixes are (aa) and (a) and (). The longest of these that exists in the graph is (a). So there is a blue arc from (caa) to (a).
3.3.5 Green Arc
There is a green "dictionary suffix" arc from each node to the next node in the dictionary that can be reached by following blue arcs. For example, there is a green arc from (bca) to (a) because (a) is the first node in the dictionary (i.e. a blue node) that is reached when following the blue arcs to (ca) and then on to (a).
3.3.6 Match Process
At each step, the current node is extended by finding its child, and if that doesn't exist, finding its suffix's child, and if that doesn't work, finding its suffix's suffix's child, and so on, finally ending in the root node if nothing's seen before.