Data Structure

一个位置为=i=的节点,其左孩子为=2i=,父节点为⌊i/2⌋

• 若要删除的节点是一片树叶，直接删。
• 若该节点有一个子节点，用该子节点代替它。
• 若有两个子节点，使用其右子树中最小的数据代替该节点，再将那个最小的数据的节点（此时是空的）删除（它没有左子树）。

如果删除的次数不多，通常使用=惰性删除=:当一个元素被删除时,它仍留在树中,只是做了删除的标记.

下图中X比Z深2,需要修复.

• 把=k1=拎起来
• =Y=挂到=k2=的左子树上

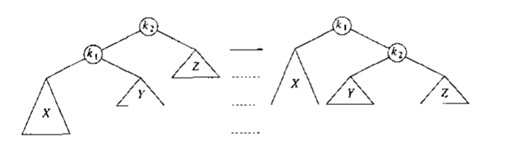
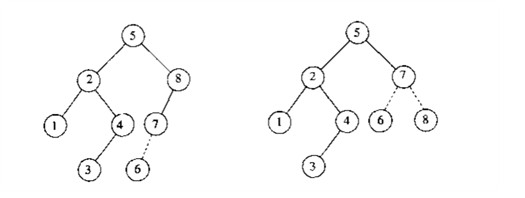
下面是一个实际的例子

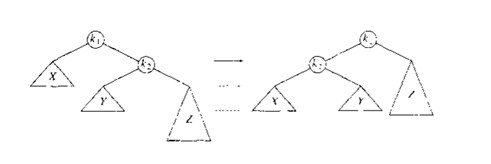
k2那个分支太深了,单旋转解决不了.双旋转修复法:

• 把=k2=拎起来
• B,=C=分别放到左右子树上.

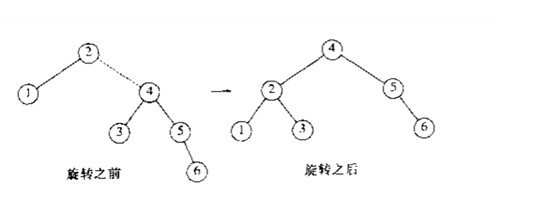
下面是实际的例子.

DeleteMin 输出结果时,要使用另一个数组.可以避免的.方法是将出来的放到最后新空出来的空穴中. 这样就会最终得到一个递减的序列.

为了得到递增的序列,可以使用=max堆=,即根是最大的.

已知枢纽元,如何将小的放前面,大的放后面?

1. 将枢纽元与最后的元素交换
2. i 指向第一个元素, j 指向倒数第二个元素
3. 将 i 右移,移过比枢纽元小的元素.将 j 左移,移过比枢纽元大的元素
4. 当 i 和 j 都停止时,交换 i 和 j 的数据,并重复步骤 3
5. 当 i 和 j 交错了,即 i 跑到 j 的右侧了,将i的值和枢纽元交换

1. 在图中找到一个入度为0的点
2. 将它的邻接点得入度–
3. 将它放入拓扑序列中

for(all vertex) {
  v = findVertexOfIndegreeZero();
  for each w adjacent to v {
    Indegree[w]--;
  }
}

使用队列的算法

q = createQueue(N);
MakeEmpty(q);
for each vertex v {
  if (Indegree[v]==0) Enqueue(V,Q);
}
while(!IsEmpty(q)) {
  v = Dequeue(q);
  for each w adjacent to v {
    if (--Indegree[v]==0) Enqueue(w,q);
  }
}

所有边的权值为1.

对于每一个顶点,记录3个值:

• Known: 当前节点有没有被访问过.有则置1
• dv: 当前已知的最短距离
• pv: 路径的上一个节点

一个不太好的算法

1. 取起始点,其dv设为0
2. currDist递增,初值为0.
3. 将当前dv为currDist且没有访问过的节点,访问之: 设置其所有邻接节点的dv和pv;
4. 重复2

void Unweighted(Table t) {
  int currDist;
  Vertex v,w;
  for (currDist=0;currDist<Num; currDist++) {
    for each vertex v {
      if (!t[v].Known && t[v].Disk == currDist) {
        t[v].known = 1;
        for each w adjacent to v {
          if (t[w].dist == Infinity) {
            t[w].dist = currDist+1;
            t[w].path = v;
          }
        }
      }
    }
  }
}

更好点的算法

1. 创建一个空队列,将初始节点放入
2. 队列出队,访问: 设置所有邻接点得dv和pv; 将所有邻接点加入队列
3. 重复2

void Unweighted(Table t) {
  Queue q;
  Vertex v,w;
  q = CreateQueue(N);
  MakeEmpty(q);
  Enqueue(s,q);
  while(!IsEmpty(q)) {
    v = Dequeue(Q);
    t[v].known = 1;
    for each w adjacent to v {
      if (t[w].dist == Infinity) {
        t[w].dist = t[v].dist + 1;
        t[w].path = v;
        Enqueue(W,Q);
      }
    }
  }
}

解决单源最短路径问题的一般方法叫做 Dijkstra算法.

1. 选取一个起始点,标记其dv为0
2. 访问一个known为0的点,标记其known为1,更新其邻接的所有known为0的点得dv.

步骤:

1. 选取一个初始点,做为树的根
2. 选取一个不在树中得点,要求: 它到树中得节点的距离是其他不在树中节点中最小的.
3. 将这个点加入树中.

对每个节点,维护3个值:

• known
• dv: 该节点到树中节点的最短路径
• pv: 到哪个节点

算法步骤:

1. 选初始点,放入树中当根
2. 对树中的但是known为0的点,去dv最小的一个,访问: known设为1; 更新其邻接的所有点得dv和pv;

在所有边上,选择最小的,如果它加入树中,不构成圈,则加入到树中.

算法:

• 把图种所有边,构建成一个堆
• 不断DeleteMin,测试该边的两个顶点是否在同一个集合中.如果在,则不能添加,会成圈.不在,则加入.